引入

在 OI 中，我们常见一类问题，这类问题需要你维护并统计所有的环的信息（比如求所有环的总长度）。我们知道，一个 $n$ 个点 $m$ 条边的图，最高能有 指数级 (?) 个环，所以显然枚举每一个环并计算贡献的方案是不可取的，于是我们需要一个方法能够统计所有环的信息。

前置知识：DFS 树

给定一个图，我们可以按照 DFS 的方法遍历这个图（不重复访问已经访问过的点），将会得到一个 DFS 树。如图，是在一个有向图上进行 DFS 后，生成的 DFS 树，其中实线代表DFS 树上的边，简称树边，虚线因为连向了已经访问过的点，代表不在 DFS 树上的边，简称非树边。你可能会发现，这些非树边的颜色不一样，他们代表的是不同种类的非树边，具体来说：

1. 红色边代表返祖边，因为它连向了自己的祖先。
2. 绿色边代表前向边，因为他连向了自己的子孙，但是由于我们进行的是深度优先搜索，所以这条边指向的节点已经被访问过。
3. 蓝色边代表横叉边，因为他连向了其他子树的节点。

特别的，在无向图中，只有树边和返祖边。

性质

这里给出一个结论：对于某些特定的信息（如异或）等，我们通过只有一条非树边所产生的环，他们的信息可以组合出所有的环。

我们将通过几道例题让读者认识到这点。

例题 1：LG4151 最大XOR和路径

题意简述

考虑一个边权为非负整数的无向连通图，节点编号为 $1\sim n$，试求出一条从 $1\to n$ 的路径，使得路径上经过的边的权值的 XOR 和最大。

$n\le 50000,m\le 100000$，边权 $10^{18}$。

题解

本题需要你有一个前置知识：线性基。如果你不知道线性基是什么，你可以简单理解成一个「将一些数丢进去，算出选取其中几个后的异或最大值」的工具。关于线性基是什么，你可以去 OI-Wiki 上查阅或查看 mcx 学长的题解。

由于异或拥有一个性质：经过一条路径两次就相当于没有经过这条路径（$x\oplus x=0$），所以我们最终的路径在异或消去后一定形如下图：

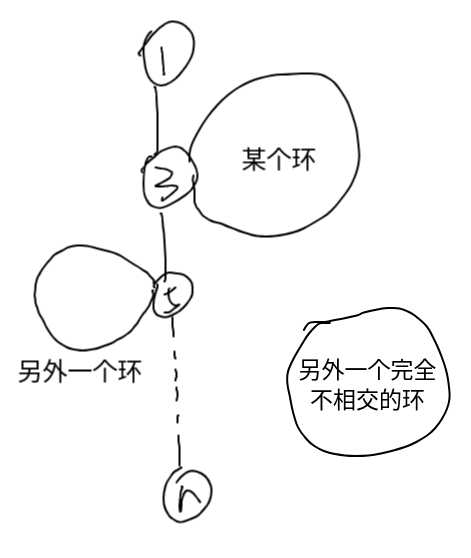
即：一条 $1\to n$ 的路径与某几个环的异或。再思考一下，我们可以发现，这个 $1\to n$ 的路径选取哪一条对我们的答案根本没有影响，如下图：

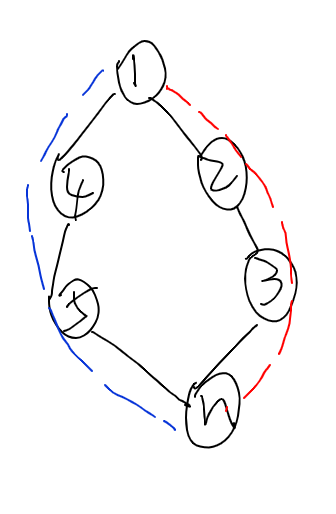
假设你选取了红色路径（也就是 $1\to2\to 3\to n$），但实际上答案选择的路径是蓝色路径，那么你完全可以将答案看成「红色路径」与「红色路径+蓝色路径形成的环（也就是 $n\to 3\to 2\to 1\to 4\to 5\to n$）」的异或，由于红色路径被走了两遍，所以相当于没走。

接下来的问题就在于，如何求出所有环的异或值，并放进线性基里求出答案？

由我们之前给出的结论，我们大胆猜测所有「只有一条非树边组成的环」可以表示出所有的环的异或情况，如图。

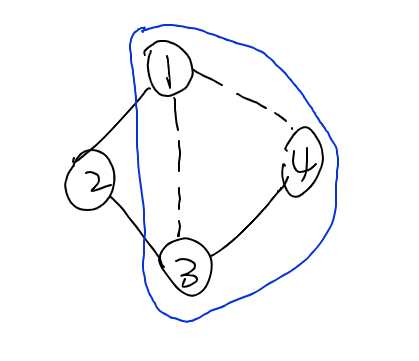
在这个图上，我们有一个环 $1\to 3\to 4 \to 1$，他拥有两条非树边 $(1,3),(1,4)$，于是我们可以用 $1\to 2\to 3\to 4\to 1$ 和 $1\to2 \to 3\to 1$ 相异或，可以得到这个环。

同样的，可以证明，对于任意的一个环，我们都可以用只有一条非树边的环将他表示，于是我们只需要在 DFS 的过程中构造线性基就可以解决这题了。

const int MAXN = 5e4 + 5;
struct _node {
	int v, w;
};
int n, m, p[80], xr[MAXN];
bool vis[MAXN];
vector<_node> G[MAXN];

void insert(int x) {
	for (int i = 62; i >= 0; --i) {
		if ((x >> i) & 1) {
			if (p[i]) x ^= p[i]; 
			else return p[i] = x, void();
		} 
		if (!x) return;
	}
}

void dfs(int x, int fa, int s) {
	xr[x] = s; vis[x] = true;
	for (auto [u, w]:G[x]) {
		if (vis[u]) insert(s ^ w ^ xr[u]); // 将当前这个环插入到线性基中
		else dfs(u, x, s ^ w);
	}
}

void work() {
	cin >> n >> m;
	for (int i = 1; i <= m; ++i) {
		int u, v, w; cin >> u >> v >> w;
		G[u].push_back({v, w}), G[v].push_back({u, w});
	}
	dfs(1, 0, 0);

    int ans = xr[n];
	for (int i = 62; i >= 0; --i) ans = max(ans, ans ^ p[i]); // 线性基
	cout << ans << endl;
}

例题 2：CF1515G Phoenix and Odometers

题意

给定一个 $n$ 个点 $m$ 条边的带权有向图，多次询问给定 $p,s,t$，求是否存在一条从 $p$ 出发回到 $p$ 的路径使得路径的边权和 $w$ 满足 $(w+s)\bmod t=0$。

$n,m,q\le 2\times 10^5$。

题解

首先由于你要从 $p$ 出发并且回到 $p$，所以你经过的所有点一定是和 $p$ 处于一个强连通分量里（否则你走出强联通之后无法回到 $p$）。所以我们可以对每个强连通分量分别考虑。

对于任意模数 $t$（即使我们还不知道 $t$ 具体是什么），我们都有（注意下方的讨论如无标注均在模意义下进行）：

1. 如果存在一条 $a\to b$ 的路径长度为 $w$，那么存在一条 $b\to a$ 的路径长度为 $-w$。证明：假设 $b\to a$ 的路径长度为 $w'$，那么我们可以从 $b$ 经过 $a$ 绕回 $b$ 走 $t$ 次，再从 $b$ 走到 $a$，最终的长度为 $tw'+(t-1)w\equiv -w\pmod t$。
2. 如果 $a$ 在一个大小为 $x$ 的环内，那么对于该强连通分量里的任意一个点 $b$，$b$ 也在大小为 $x$ 的环内。证明：设 $b\to a$ 路径长度为 $w$，则构造形如 $b\to a\to a \to b$ 的路径，长度为 $w+x+(-w)=x$。

由于我们要求是否存在一个边权和为 $w$ 使得 $(w+s)\bmod t=0$，一个非常朴素的想法是我们求出一个强连通分量里的所有的环，设所有环的大小为 $x_1,x_2,\cdots x_n$，对于一组询问，我们其实想知道是否存在 $n$ 个整数 $k_1,k_2,\cdots,k_n$ 满足 $(k_1x_1+k_2x_2+\cdots+k_nx_n)+s\equiv 0\pmod t$。通过裴蜀定理可知，存在 $k_1,k_2,\cdots,k_n$ 的充要条件是 $s$ 为 $\gcd(x_1,x_2,\cdots,x_n)$ 的倍数。

但是求出每一个环显然是不太现实的。注意到有些 $x$ 显然是不必要的（比如一个 $x_i$ 是另一个 $x_j$ 的倍数），于是我们考虑是否可以「精简」一下我们的 $x_1,x_2,\cdots x_n$，选出其中的一个子集，使得原先可以表示出的任意一个环在子集中也可以表出。

我们求出一个强连通分量的 DFS 生成树，设根节点为 $r$，对于任意节点 $x$ 记从 $r$ 到 $x$ 的路径边权和为 $dep_x$。我们发现，对于两个点 $x,y$，设他们之间的路径长度为 $w$，$x\to y\to x$ 的这个环可以表示为 $dep_x+w-dep_y$，通过归纳法可以证明：对于任意一个环，均可以被若干个「形如 $r\to x\to y\to r$ 的环」表出，其中 $x,y$ 之间有连边。

所以我们就可知，要想求处所有环的 $\gcd$，只需要求出「形如 $r\to x\to y\to r$ 的环」即可。

最终对于每次询问 $p,s,t$，设我们要找的环长度为 $w$，即 $w=(k_1x_1+k_2x_2+\cdots+k_nx_n)=k\gcd(x_1,x_2,\cdots,x_n),k\in \mathbb{Z}$，我们有 $s=bt-aw$，其中 $a,b\in \mathbb{Z}+$，由裴蜀定理可知存在 $a,b$ 使得该式成立的充要条件为 $\gcd(t, w)|s$，也即 $\gcd(t,\gcd(x_1,x_2,\cdots,x_n))|s$。

最终时间复杂度为 $O(n\log V)$，视 $n,m,q$ 同阶。

int n, m, q, st[MAXN], top, dfn[MAXN], g[MAXN], low[MAXN], dep[MAXN], col[MAXN], tot, scc;
struct _node {
    int v, w;
};
struct _edge {
    int u, v, w;
} e[MAXN];
vector<_node> G[MAXN], T[MAXN];
bool vis[MAXN], inst[MAXN];

void tarjan(int x) {
    dfn[x] = low[x] = ++tot;
    st[++top] = x;
    inst[x] = true;
    for (auto [u, w]:G[x]) {
        if (inst[u]) low[x] = min(low[x], dfn[u]);
        else if (!dfn[u]) {
            tarjan(u);
            low[x] = min(low[x], low[u]);
        }
    }
    if (low[x] == dfn[x]) {
        col[x] = ++scc;
        inst[x] = 0;
        while (st[top] != x) {
            col[st[top]] = col[x];
            inst[st[top]] = 0;
            top--;
        }
        top--;
    }
}

void dfs(int x) {
    vis[x] = true;
    for (auto [u, w]:G[x]) {
        if (vis[u] || col[u] != col[x]) continue;
        dep[u] = dep[x] + w;
        dfs(u);
    }
}

void work() {
    cin >> n >> m;
    for (int u, v, w, i = 1; i <= m; ++i) {
        cin >> u >> v >> w;
        G[u].push_back({v, w});
        e[i] = {u, v, w};
    }
    for (int i = 1; i <= n; ++i)
        if (!dfn[i]) tarjan(i);
    for (int i = 1; i <= n; ++i)
        if (!vis[i]) dfs(i);
    for (int i = 1; i <= m; ++i) {
        auto u = e[i].u, v = e[i].v, w = e[i].w;
        if (col[u] != col[v]) continue;
        if (!g[col[u]]) g[col[u]] = dep[u] + w - dep[v];
        else g[col[u]] = __gcd(g[col[u]], dep[u] + w - dep[v]);
    }
    cin >> q;
    while (q--) {
        int p, s, t;
        cin >> p >> s >> t;
        if (s % t != 0 && !g[col[p]]) cout << "NO" << endl;
        else if (s % __gcd(t, g[col[p]]) == 0) cout << "YES" << endl;
        else cout << "NO" << endl;
    }
}

例题 3：BZOJ4424 Fairy (CF19E 加强版)

题意

给定 $n$ 个点 $m$ 条边的图，求出删掉一条边，使得这个图变成二分图的方案数。

$n,m\le 10^6$。

题解

二分图的判定定理：一个图是二分图当且仅当他没有奇环。

我们要删掉一条边，使得这个图上不再有奇环，所以我们选择的边必须要是这些奇环的边的交集中的一个，特别的，当图中没有奇环时，任意删掉一条边都是答案。

但是我们删掉一条边，可能会产生新的环，如图：

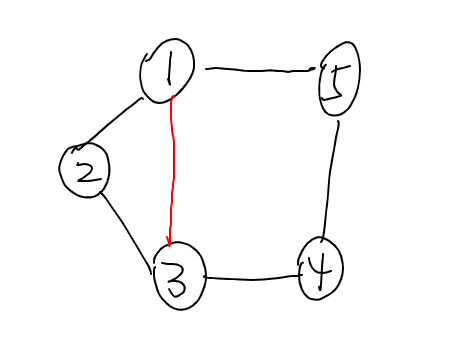
当我们删掉了红色边后，反而产生了新的奇环 $1\to 2\to 3\to 4\to 5\to 1$，观察发现，奇环+奇环=偶环，奇环+偶环=奇环，所以我们断掉的边还不能是处于一个偶环中。

于是我们在断掉处于奇环的交集中的边的同时，还不能断掉处于任意一个偶环中的边，否则就会产生新的奇环。

那么怎么求出所有奇环的交集？枚举每个奇环是不现实的，所以我们仍然使用上面的结论：可以通过「只有一条非树边的环」组成所有的环。

最后只需要套一个树上差分，就可以解决这道题，注意特判只有一个奇环的情况，此时这条非树边断掉也是可以删掉奇环的，否则非树边就永远不能成为答案。

const int MAXN = 2e6 + 5;
int n, m, cnt, col[MAXN], s[MAXN], ans[MAXN], anscnt;
struct _node {
	int v, id;
};
vector<_node> G[MAXN];
bool vis[MAXN], edg[MAXN], isodd[MAXN];

void dfs(int x) {
	vis[x] = true;
	for (auto [u, id]:G[x]) {
		if (!vis[u]) {
			col[u] = col[x] ^ 1;
			edg[id] = true;
			dfs(u);
		} else if (!edg[id]) {
			edg[id] = true;
			if (col[u] == col[x]) { // odd loop
				cnt++;
				isodd[id] = true;
				s[u]--, s[x]++;
			}
			else {
				s[u]++, s[x]--;
			}
		}
	}
}

void calc(int x) {
	vis[x] = true;
	for (auto [u, id]:G[x]) {
		if (!vis[u]) {
			calc(u);
			if (s[u] == cnt) ans[++anscnt] = id;
			s[x] += s[u];
		}
	}
}

void work() {
	cin >> n >> m;
	for (int i = 1, u, v; i <= m; ++i) {
		cin >> u >> v;
		G[u].push_back({v, i});
		G[v].push_back({u, i});
	}
	for (int i = 1; i <= n; ++i)
		if (!vis[i]) dfs(i);
	if (!cnt) {
		cout << m << endl;
		for (int i = 1; i <= m; ++i) cout << i << ' ';
		cout << endl;
		return;
	}
	if (cnt == 1) {
		for (int i = 1; i <= m; ++i)
			if (isodd[i]) ans[++anscnt] = i;
	}
	fill(vis + 1, vis + 1 + n, false);
	fill(edg + 1, edg + 1 + m, false);
	for (int i = 1; i <= n; ++i)
		if (!vis[i]) calc(i);
	sort(ans + 1, ans + 1 + anscnt);
	cout << anscnt << endl;
	for (int i = 1; i <= anscnt; ++i)
		cout << ans[i] << ' ';
	cout << endl;
}