​深度优先搜索算法​（英语：Depth-First-Search，简称​DFS​）是一种用于遍历或搜索树或图的算法。沿着树的深度遍历树的节点，尽可能深的搜索树的分支。当节点v的所在边都己被探寻过，搜索将回溯到发现节点v的那条边的起始节点。这一过程一直进行到已发现从源节点可达的所有节点为止。如果还存在未被发现的节点，则选择其中一个作为源节点并重复以上过程，整个进程反复进行直到所有节点都被访问为止。属于盲目搜索。

深度优先搜索是图论中的经典算法，利用深度优先搜索算法可以产生目标图的相应拓扑排序表，利用拓扑排序表可以方便的解决很多相关的图论问题，如最大路径问题等等。（摘自wiki百科）

简要概括，深度优先的主要思想就是“不撞南墙不回头”，“一条路走到黑”，如果遇到“墙”或者“无路可走”时再去走下一条路。

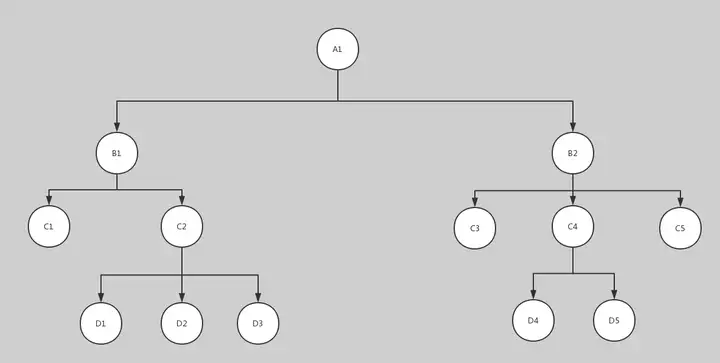
关键在“深度优先”，如上图所示，假设我们在A1的位置，且没有上帝视角（想象自己处在一个迷宫里），想要走到D5的位置，该怎么办？ 最开始，摆在我们面前的有两条路—B1、B2，我们先假设D5在最左边第二层即B1的位置（虽然D5在最右边的最后一层，但这些都不重要，不要在意这些细节）；我们跟着心中的信仰走到了B1的位置，发现这里是B1并不是D5。这时我们有三条路可以走，接着往下走的C1、C2和走到同级B2的位置；因为我们是深度优先，所以选择一条路走到黑，于是我们选择继续跟随自己的信仰，往下走，且选择左边的C1。走到C1，发现再往下没路了，这时可选路径是返回B级或者走向同级的C2；依照DFS原则，我们选择C2，接下来的步骤跟上面一样，依次遍历D1、D2、D3三个点再返回C级、B级最后到B2，开始新一轮的深度遍历，直到找到D5。

深搜的思想就是这样“不撞南墙不回头”、“一条路走到黑”，下面通过代码实例化深搜。

最经典的莫过于迷宫问题。

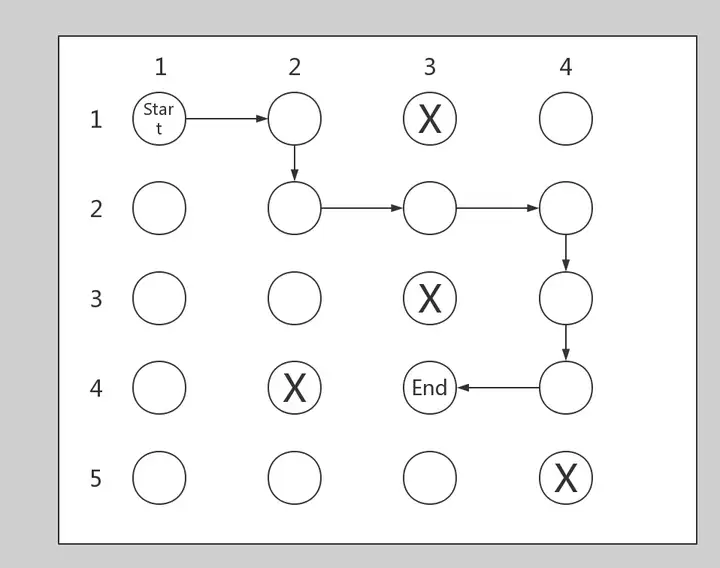
假设现在有一个4 * 5的小型迷宫，Start为起点、End为终点、X为障碍物，如何找到从起点到终点的最短路径？

我们可以先用一个二维数组来存储这个迷宫，问题便简化为寻找从（1，1）到（p，q）的最短路径。

当我们从起点出发时，有两条路可以选择，即向右或向下。实际上，在这个迷宫里，我们每一步的选择都只有四种类型，即向上下左右四个方向走。我们在这里设定一个顺序，按照顺时针，右、下、左、上的顺序依次尝试。

代码实现很简单，定义一个方向数组即可。

int next[4][2] = {{0, 1}, //向右走
                    {1, 0}, //向下走
                    {0, -1}, //向左走
                    {-1, 0}}; //向上走

通过这个方向数组的循环，很容易获得下一步的坐标，这里用x、y表示当前横坐标和纵坐标，用tx、ty存储下一步的横坐标和纵坐标。

for(k = 3; k <= 3; k++){
    //计算下一步点的坐标
    tx = x + next[k][0];
    ty = y + next[k][1];
}

根据上面介绍的深搜策略，我们先往右边走，来到（1，2）这个点。因为（1，3）这个点是障碍物无法到达，（1，1）是刚才来的路径中已经走过的点，所以只能到（2，2）这个点，以此类推，继续往下走。这里需要注意的是我们并不是走到终点便立即结束，因为刚才只尝试了一条走法，并不一定是最短的。刚才很多地方再悬着方向的时候都有很多种选择，因此我们需要返回到这些地方继续尝试往别的方向走，直到把所有可能都尝试一边，最终输出最短的一条路径。例如下图就是一种可行的方案

实现上诉思想的关键点在于判断当前位置和找出下一步的方向，我们可以定义一个函数通过递归实现，其中x，y表示当前坐标，step代表已经走过的步数，p，q代表终点位置。

void dfs(int x, int y, int step){
    //判断是否到达终点
    if(x == p && y == q){
        //更新最小值
        if(step < min)
            min = step;
        return;
    }
    return;
}

另外，我们还需要对下一个点进行一些判断，包括是否越界，是否为障碍物，是否已经在路径中。这里用数组book [tx][ty]来记录格子(tx, ty)是否已经在路径中。假如这个点符合所有的要求，就对这个点进行下一步的扩展即递归dfs（tx, ty, step + 1）。

实现代码如下，其中设非障碍物的迷宫数组元素为0

for(k = 0; k <= 3; k++){
        //计算下一个点的坐标
        tx = x + Next[k][0];
        ty = y + Next[k][1];

        //判断是否越界
        if(tx < 1 || tx > n ||ty < 1 || ty > m)
            continue;

        //判断改点是否为障碍物或者已经在路径中
        if(a[tx][ty] == 0 && book[tx][ty] == 0){
            book[tx][ty] = 1; //标记这个点已经走过
            dfs(tx, ty, step + 1); //开始尝试下一个点
            book[tx][ty] = 0; //尝试结束，取消这个点的标记
        }
    }

下面是完整代码，基本上很多裸题改下数据就能A

#include <bits/stdc++.h>
using namespace std;
int n, m, p, q, minn = 9999999;
int a[51][51], book[51][51];
int Next[4][2] = {{0, 1}, //向右走
                    {1, 0}, //向下走
                    {0, -1}, //向左走
                    {-1, 0}}; //向上走

void dfs(int x, int y, int step){
    int tx, ty, k;
    //判断是否到达终点
    if(x == p && y == q){
        //更新最小值
        if(step < minn)
            minn = step;
        return;
    }

    //枚举四种走法
    for(k = 0; k <= 3; k++){
        //计算下一个点的坐标
        tx = x + Next[k][0];
        ty = y + Next[k][1];

        //判断是否越界
        if(tx < 1 || tx > n ||ty < 1 || ty > m)
            continue;

        //判断改点是否为障碍物或者已经在路径中
        if(a[tx][ty] == 0 && book[tx][ty] == 0){
            book[tx][ty] = 1; //标记这个点已经走过
            dfs(tx, ty, step + 1); //开始尝试下一个点
            book[tx][ty] = 0; //尝试结束，取消这个点的标记
        }
    }
    return;
}

int main(){
    int startx, starty;
    //读入n行m列的迷宫 1为障碍物 0为非障碍物
    cin >> n >> m;
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= m; j++)
            cin >> a[i][j];

    //读入起点和终点坐标
    cin >> startx >> starty >> p >> q;

    //从起点开始搜索
    book[startx][starty] = 1; //标记起点已经在路径中，防止后面重复走
    //初始步数为0
    dfs(startx, starty, 0);

    //输出
    cout << minn;
    return 0;
}


/********
Sample Input：
5 4
0 0 1 0
0 0 0 0
0 0 1 0
0 1 0 0
0 0 0 1
1 1 4 3


Sample Output：
7
********/

关于搜索，NYOJ上有专门的分类，这个模板还是能A不少水题的，推荐先从NYOJ 32、NYOJ 58、NYOJ 488练手，剩下的看心情刷就好（还是喜欢NSWOJ 无奈没有分类外加需要校园网 sadQAQ）